Cocos Creator 3.0: 3D camera follow and rotate
This article is translated and reprinted from Cocos Chinese community, Author: JoeyHuang312.
After the official version of Cocos Creator 3.0 was updated, many developers began to try to do simple things on the camera. Nowadays, FPS-like games are very popular, and the camera following technology is indispensable to learn. By learning quaternions, understanding the rotation of the camera, to achieve the common first-person and third-person perspectives in games.
01 Initial exploration
Cocos 3D’s quaternion class Qaut.ts helps us encapsulate the basic quaternion calculations, algorithms and related formulas.
Although the topic of our article is following and rotating, in fact, most of it is for quaternion rotation. For those who are new to quaternion numbers, it may be a little unfamiliar, and it is not so easy to use. Let’s talk about how to use the Quat class for several methods:
// static rotateY<Out extends IQuatLike>(out: Out, a: Out, rad: number): Out;
// The first parameter of many methods in Quat has an output parameter, which
// represents the quaternion to be output after the current calculation. Of
// course, his return value is also the calculated quaternion.
// The following sentence means to rotate the specified angle around the Y axis,
// the unit in the method is calculated in radians, so it needs to be converted.
this.node.rotation=Quat.rotateY(new Quat(),this.node.rotation,this.currAngle*Math.PI/180);
// The method is to obtain the quaternion according to Euler angle, the unit of
// Euler angle is angle.
this.node.rotation=Quat.fromEuler(new Quat(),this.angleY,this.angleX,0);
// Rotate the quaternion around the specified axis in world space, in radians,
// around the UP axis.
Quat.rotateAround(_quat,this.node.rotation,Vec3.UP,rad);
Speaking of the rotateAround method, we can clearly see through the picture that given the original quaternion, as well as the rotation axis and angle (the method uses radians as the unit), we can determine the rotation around this axis. The quaternion is the position after rotation.
As for the specific calculation principles, any search engine has a lot of formulas for calculating quaternions. For a deeper understanding, search for additional reading on quaternion knowledge. This article mainly focuses on the camera following the rotation angle of view.
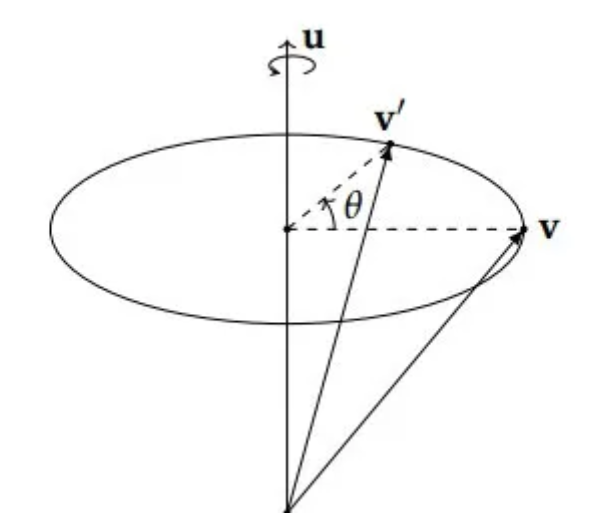
Take a look at the source code of these three methods:
public static rotateY<Out extends IQuatLike> (out: Out, a: Out, rad: number) {
rad *= 0.5;
const by = Math.sin(rad);
const bw = Math.cos(rad);
const { x, y, z, w } = a;
out.x = x * bw - z * by;
out.y = y * bw + w * by;
out.z = z * bw + x * by;
out.w = w * bw - y * by;
return out;
}
public static rotateAround<Out extends IQuatLike, VecLike extends IVec3Like> (out: Out, rot: Out, axis: VecLike, rad: number) {
// get inv-axis (local to rot)
Quat.invert(qt_1, rot);
Vec3.transformQuat(v3_1, axis, qt_1);
// rotate by inv-axis
Quat.fromAxisAngle(qt_1, v3_1, rad);
Quat.multiply(out, rot, qt_1);
return out;
}
public static fromEuler<Out extends IQuatLike> (out: Out, x: number, y: number, z: number) {
x *= halfToRad;
y *= halfToRad;
z *= halfToRad;
const sx = Math.sin(x);
const cx = Math.cos(x);
const sy = Math.sin(y);
const cy = Math.cos(y);
const sz = Math.sin(z);
const cz = Math.cos(z);
out.x = sx * cy * cz + cx * sy * sz;
out.y = cx * sy * cz + sx * cy * sz;
out.z = cx * cy * sz - sx * sy * cz;
out.w = cx * cy * cz - sx * sy * sz;
return out;
}
In fact, the first parameter is a bit redundant, because one more parameter must be added every time. In order to make it easier to use, I wrote a quaternion class myself, and removed the first parameter.
Note: There is a Quaternion class in the article that I encapsulated, which is similar to Quat, which is available in the source code of the original text.
02 Surround the object
In Cocos 3D rotating around the object, there is nothing to say, just a few lines of code, the relevant instructions are also commented.
update(dt:number)
{
// Revolve around
Quaternion.RotationAroundNode(this.node,this.target.position,Vec3.UP,0.5);
this.node.lookAt(this.target.position);
}
This method is similar to the Quat.rotateAround method above, except that a modified position is encapsulated here, so that Node can get the position change position according to this rotation arc.
Here we talk about the RotationAroundNode method, because I will get it later, here I have directly encapsulated RotationAroundNode in a class (the source code is behind the original text), and the specific implementation method inside is:
/**
* Rotate the transformation by angle degrees around the axis passing
* through the point in world coordinates.
* This will modify the position and rotation of the transformation.
* @param self to transform the rotation target
* @param pos specifies the surrounding point
* @param axis rotation axis
* @param angle rotation angle
*/
public static RotationAroundNode(self:Node,pos:Vec3,axis:Vec3,angle:number):Quat
{
let _quat=new Quat();
let v1=new Vec3();
let v2=new Vec3();
let pos2:Vec3=self.position;
let rad=angle* this.Deg2Rad;
// Calculate the quaternion based on the axis of rotation and
// the arc of rotation
Quat.fromAxisAngle(_quat,axis,rad);
// Subtract, the vector between the target point and the camera point
Vec3.subtract(v1,pos2,pos);
// Rotate the vector dir according to the calculated quaternion, and then
// calculate the rotated distance
Vec3.transformQuat(v2,v1,_quat);
self.position=Vec3.add(v2,pos,v2);
// Rotate the quaternion around the specified axis in world space
// according to the axis and radian
Quat.rotateAround(_quat,self.rotation,axis,rad);
return _quat;
}
This code is more difficult to digest if you don’t understand the principle of quaternion. Of course, you can use it directly without any problems. However, it is recommended that you understand the concept of quaternion and have a deep understanding of 3D rotation.
03 FPS essential-first person follower
First-person perspective, for example, when we are playing a racing car, we will have two perspectives, one is to look forward from the outside of the car, and the other is to look out of the car from the inside of the car with ourselves as the center.
-
Very simple two sentences of code, first set the Euler angle according to the offset of the mouse, and then convert the Euler angle to a quaternion and assign it to the camera
-
The X direction of the mouse here means rotation around the Y axis, and the Y direction of the mouse means rotation around the X axis. All the assignment conversions are reversed.
-
When the camera looked up and lowered, I also made a limit angle:
private MouseMove(e: EventMouse) {
this.angleX+=-e.movementX;
this.angleY+=-e.movementY;
console.log(this.angleY);
this.angleY=this.Clamp(this.angleY,this.xAxisMin,this.xAxisMax);
//this.node.rotation=Quat.fromEuler(new Quat(),this.angleY,this.angleX,0);
// Euler angles converted to quaternions
this.node.rotation=Quaternion.GetQuatFromAngle(new Vec3(this.angleY,this.angleX,0));
return ;
}
The third-person follower from the perspective of God, it seems that different games have different follow methods. Here I will list three first.
04 A Simple Follow
This is a very simple follow. Set the height and distance from the target, get the target position the camera will go to, and then perform interpolation operations on the camera.
let temp: Vec3 = new Vec3();
Vec3.add(temp, this.lookAt.worldPosition, new Vec3(0, this.positionOffset.y, this.positionOffset.z));
this.node.position = this.node.position.lerp(temp, this.moveSmooth);
05 Trailing behind
It seems that many RPG games have this kind of angle of view, always following behind, the camera cannot be rotated at will, it will automatically rotate according to the front direction of the character.
Specific instructions are also in the comments below, and there seems to be nothing to say. The two lines of code commented are from the original method of Cocos 3D. I used the encapsulation method that I slightly modified myself.
// calculate the coordinates of the location of the camera from the target
// first, how high is the distance Y, how far is Z
// The following four sentences are equivalent to:
// targetPosition+Up*updistance-forwardView*backDistance
let u = Vec3.multiplyScalar(new Vec3(), Vec3.UP, this.positionOffset.y);
let f = Vec3.multiplyScalar(new Vec3(), this.target.forward, this.positionOffset.z);
let pos = Vec3.add(new Vec3(), this.target.position, u);
// Originally, it should be subtracted, but the lookat below defaults
// to -z in front of it, and all here is reversed to add
Vec3.add(pos, pos, f);
// Spherical difference moves, I found that cocos only moves Lerp difference,
// but I think Unity has SmoothDampV3 smooth buffer movement, so I copied a
// spherical difference here
this.node.position = VectorTool.SmoothDampV3(this.node.position, pos, this.velocity, this.moveSmooth, 100000, 0.02);
//cocosdifference shift
//this.node.position=this.node.position.lerp(pos,this.moveSmooth);
// Calculate the front direction
this.forwardView = Vec3.subtract(this.forwardView, this.node.position, this.target.getWorldPosition());
//this.node.lookAt(this.target.worldPosition);
this.node.rotation=Quaternion.LookRotation(this.forwardView);
-
In order to better achieve a certain easing effect in the game, we must use interpolation. If it is just a simple binding of the relationship, the effect will be very blunt, but after we add the interpolation calculation, the buffering effect of the lens can be well achieved.
-
Lerpis linear interpolation, which performs interpolation calculation between two points and moves. -
SmoothDampV3smoothly buffers, things are not stiff movement but decelerate buffering movement to a specified position,Lerpis more like a linear decay, andSmoothDampis like an arc decay, both are from fast to slow.
The last two lines of code are aimed at the camera’s direction. The principles of the two lines of code are the same:
let _quat = new Quat();
Vec3.normalize(_forward,_forward);
// Calculate the quaternion based on the front and up directions of the viewport
Quat.fromViewUp(_quat,_forward,_upwards);
If you want to see more in-depth code principles, you can check the Cocos source code, the specific source code location is:
Window location: F:\CocosDashboard\resources.editors\Creator\3.0.0\resources\resources\3d\engine\cocos\core\math\quat.ts
Mac location: /Applications/CocosCreator/Creator/3.0.0/CocosCreator.app/Contents/Resources/resources/3d/engine/bin/.cache/dev/editor/transform-cache/fs/cocos/core/math/quat.js
06 Spin Freely
This can be said to be an upgraded version of the above one, because when this is following, the camera can be rotated up and down, left and right according to the mouse, and the target will walk according to the positive direction of the camera.
Note: Need to match the rotation code related to the target person to use, the source code stamps the original text at the end.
/**
* Set the position of the camera from the target in real time
*/
public SetMove() {
this._forward = new Vec3();
this._right = new Vec3();
this._up = new Vec3();
Vec3.transformQuat(this._forward, Vec3.FORWARD, this.node.rotation);
//Vec3.transformQuat(this._right, Vec3.RIGHT, this.node.rotation);
//Vec3.transformQuat(this._up, Vec3.UP, this.node.rotation);
this._forward.multiplyScalar(this.positionOffset.z);
//this._right.multiplyScalar(this.positionOffset.x);
//this._up.multiplyScalar(this.positionOffset.y);
let desiredPos = new Vec3();
desiredPos = desiredPos.add(this.lookAt.worldPosition).subtract(this._forward).add(this._right).add(this._up);
this.node.position = this.node.position.lerp(desiredPos, this.moveSmooth);
}
/**
* Calculate the rotation quaternion around the X axis and Y axis
* according to the mouse X, Y offset
* @param e
*/
private SetIndependentRotation(e: EventMouse) {
let radX: number = -e.movementX;
let radY: number = -e.movementY;
let _quat: Quat = new Quat();
// Calculate the quaternion rotating around the X axis and apply
// it to the node, here is the mouse up and down Y offset
let _right = Vec3.transformQuat(this._right, Vec3.RIGHT, this.node.rotation);
_quat = Quaternion.RotationAroundNode(this.node, this.target.position, _right, radY);
// Obtain the Euler angle and limit the range of the camera's head up
// and down
this.angle = Quaternion.GetEulerFromQuat(_quat);
this.angle.x = this.angle.x > 0 ? this.Clamp(this.angle.x, 120, 180) : this.Clamp(this.angle.x, -180, -170);
Quat.fromEuler(_quat, this.angle.x, this.angle.y, this.angle.z);
this.node.setWorldRotation(_quat);
// Calculate the quaternion of the rotation around the Y axis and
// apply it to the node, here is the up and down X offset of the mouse
_quat = Quaternion.RotationAroundNode(this.node, this.target.position, Vec3.UP, radX);
this.node.setWorldRotation(_quat);
this.angle = Quaternion.GetEulerFromQuat(_quat);
this.MouseX = this.angle.y;
this.MouseY = this.angle.x;
//console.log(this.MouseX.toFixed(2),this.MouseY.toFixed(2));
}
The character target follows the rotation:
if (data.keyCode == macro.KEY.a || data.keyCode == macro.KEY.d
|| data.keyCode == macro.KEY.w || data.keyCode == macro.KEY.s) {
if (this.camera.GetType()== ThirdPersonCameraType.FollowIndependentRotation) {
let fq = Quat.fromEuler(new Quat(), 0, this.camera.MouseX, 0);
this.node.rotation = Quat.slerp(new Quat(), this.node.rotation, fq, 0.1);
}
else {
//this.node.rotation=Quat.rotateY(new Quat(),this.node.rotation,this.currAngle*Math.PI/180);
Quaternion.RotateY(this.node, this.currAngle);
}
this.node.translate(this.movemenet, Node.NodeSpace.LOCAL);
}
The code above limits the rotation around the X axis. I limited the range of the camera’s head up and down to 120 - 180 and -180 → -170.
The reason why I set these two very weird ranges is because if the camera is facing the object at 0 degrees, it is 0-180 from facing to the head, and -180-0 from facing to looking down.
Here I need to separate the code for setting the X-axis and Y-axis rotation. You can see that I have separated a lot. Maybe my method is wrong. I haven’t found a way to simplify the code. If anyone knows, please give me some advice.
In fact, reading through the full text, we can see that the most used ones are rotationAround, lookAt, transformQuat, and transformQuat. As long as you are familiar with rotation, there is nothing to be afraid of.
